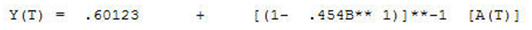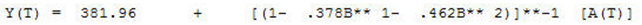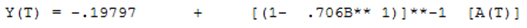The most studied time series on the planet would have to be the Box-Jenkins International Airline Passenger series found in their 1970 landmark textbook Time Series Analysis: Forecasting and Control.  Just google AirPassengers or "airline passenger arima" and you will see it all over the place. It is on every major forecasting tool's website as an example.  It is there with a giant flaw.  We have been waiting and waiting for someone to notice.  This example has let us known (for decades) that we have a something that the others don't...robust outlier detection.  Let's explore more on why and how you check it out yourself.

It is 12 years of monthly data and Box-Jenkins used Logs to adjust for the increasing variance.  They didn't have the research we have today on outliers, but what about everyone else?  I. Chang had an unpublished dissertation(look for the name Chang) at University of Wisconsin in 1982 laying out an approach to detect and adjust outliers providing a huge leap in modeling power.

It was in 1973 that Chatfield and Prothero published a paper where the words "we have concerns" regarding the approach Box-Jenkins took with the Airline Passenger time series.  What they saw was a high forecast that turned out to be too aggressive and too high.  It is in the "Introduction" section. Naively, people think that when they take a transformation and make a forecast and then inverse transform of the forecast that they are ok. Statisticians and Mathematicians known that this is quite incorrect.  There is no general solution for this except for the case of logarithms which requires a special modification to the inverse transform. This was pointed out by Chatfield in his book in 1985.  See Rob Hyndman's discussion as well.

We do question why software companies, text books and practitioners that didn't check what assumptions and approaches that previous researchers said was fact. It was "always take Logs" for the Airline series and so everyone did.  Maybe this assumption that it was optimal was never rechecked?  I would imagine with all of the data scientists and researchers with ample tools would have found this out by now(start on page 114 and read on---hint:you won't find the word "outlier" in it!). Maybe they have, but haven't spread the word?  We are now. :)

We accidently discovered that Logs weren't needed when we were implementing Chang's approach.  We ran the example on the unlogged dataset and noticed the residuals variance was constant.  What?  No need to transform??

Logs are a transformation.  Drugs also transform us.  Sometimes with good consequences and sometimes with nasty side effects.  In this case, the forecast for the Passenger was way too high and it was pointed out but went largely unnoticed(not by us).

Why did their criticism get ignored or forgotten?  Either way, we are here to tell you that across the globe in schools and statistical software it is repeating a mistake in methodology that should be fixed.

Here is the model that Autobox identifies.  Seasonal Differencing, an AR1 with 3 outliers.  Much simpler than the Regular, Seasonal Differencing, MA1, MA12 model ....with a bad forecast.  The forecast is not as aggressive.  The outlier in March 1960 is the main culprit(period 135), but the others are also important. If you limit Autobox to search for one outlier is finds the 1960 outlier, but it still uses Logs so you need to "be better". It caused a false positive F test that logs were needed.  They weren't and aren't needed!

 

 

 

 

The Residuals are clear of any variance Trend.

 

Here is a Description of the Possible Violations of the Assumptions of Constancy of the Mean and Variance in Residuals and How to Fix it.

 

Mean of the Error Changes: (Taio/Box/Chang)

1. A 1 period change in Level (i.e. a Pulse )

2. A contiguous multi-period change in Level (Intercept Change)

3. Systematically with the Season (Seasonal Pulse)

4. A change in Trend (nobody but Autobox)

Variance of the Error Changes:

5. At Discrete Points in Time (Tsay Test)

6. Linked to the Expected Value (Box-Cox)

7. Can be described as an ARMA Model (Garch)

8. Due to Parameter Changes (Chow, Tong/Tar Model)

 

It's been 6 months since ourlast BLOG.  We have been very busy.

 

We engaged in a debate on a linkedin discussion group over the need to pre-screen your data so that your forecasting algorithm can either apply seasonal models or not consider seasonal models.  A set of GUARANTEED random data was generated and given to us as a challenge four years ago.  This time we looked a little closer at the data and found something interesting. 1)you don't need to pres-creen your data 2)be careful how you generate random data

 

Here is my first response:

As for your random data, we still have it when you send it 4 years ago. I am not sure what you and Dave looked at, but if you download run the 30 day trial now and we always have kept improving the software you will get a different answer and the results posted here on dropbox.com.https://www.dropbox.com/s/s63kxrkquzc6e00/output_miket.zip

I have provided your data(xls file),our model equation (equ), forecasts(pro), graph(png) and audit of the model building process(htm).

Out of the 18 examples, Autobox found 6 with a flat forecast, 7 with 1 monthly seasonal pulse or a 1 month fixed effect, 4 with 2 months that had a mix of either a seasonal pulse or a 1 month fixed effect, 2 with 3 months that had a mix of either a seasonal pulses or a 1 month fixed effect.

Note that no model was found with Seasonal Differencing, AR12, with all 11 seasonal dummies.

Now, in a perfect world, Autobox would have found 19 flat lines based on this theoretical data. If you look at the data, you will see that there were patterns found where Autobox found them that make sense. There are sometimes seasonality that is not persistent and just a couple of months through the year.

If we review the 12 series where Autobox detected seasonality, it is very clear that in the 11 of the 12 cases that it was justified in doing so. That would make 17 of the 18 properly modeled and forecasted.

Series 1 - Autobox found feb to be low. A All three years this was the case. Let's call this a win.

Series 2 - Autobox found apr to be low. All three years were low. Let's that call this a win.

Series 3- Autobox found sep and oct to be low. 4 of the 6 were low and the four most recent were all low supporting a change in the seasonality. Let's call this a win.

Series 4- Autobox found nov to be low. All three years were low. Let's call this a win.

Series 5- Autobox found mar, may and aug to be low. All three years were low. Let's call that a win.

Series 7- Autobox found jun low and aug high. All three years matched the pattern. Let's call that a win.

Series 10 - Autobox found apr and jun to be high. 5 of the 6 data points were high. Let's call this a win.

Series 12 - Autobox found oct to be high and dec to be low. All three years this was the case. Let's call this a win.

Series 13 - Autobox found aug to be high. Two of the three years were very very high. Let's call this a win.

Series 14 - Autobox found feb and apr to be high. All three years this was the case. Let's call this a win.

Series 15 - Autobox found may jun to be high and oct low. 8 of the 9 historical data points support this, Let's call this a win.

Series 16 - Autobox found jan to below. It was very low for two, but one was quite high and Autobox called that an outlier. Let's call this a loss.

A little sleep and then I posted this response:

After sleeping on that very fun excercise, there was something that still wasn't sitting right with me. The "guaranteed" no seasonality statement didn't match with the graph of the datasets. They didn't seem to have randomness and seemed more to have some pattern.

I generated 4 example datasets from the link below. I used the defaults and graphed them. They exhibited randomness. I ran them through Autobox and all had zero seasonality and flat forecasts.

http://www.random.org/sequences/

 

 

 

It is the standard Economic Question.  Should I make or build?  The question here is: Should I build my own ARIMA modeling system or use software that can do this automatically? We lay out the general approach how to consider approaches to building a robust model.  Easier said than done does apply here.

 

Overview

Autoregressive Integrated Moving Average (ARIMA) is a process designed to identify a weighted moving-average model specifically tailored to the individual dataset by using time series data to identify a suitable model. It is a rear-window approach that doesn’t use user-specified helping variables; such as price and promotion.  It uses correlations within the history to identify patterns that can be statistically tested and then used to forecast.  Often we are limited to using only the history and no causals whereas the general class of Box-Jenkins models can efficiently incorporate causal/exogenous variables (Transfer Functions or ARIMAX).

This post will introduce the steps and concepts used to identify the model, estimate the model, and perform diagnostic checking to revise the model. We will also list the assumptions and how to incorporate remedies when faced with potential violations.

Background

Our understanding of how to build an ARIMA model has grown since it was introduced in 1976 (1).  Properly formed ARIMA models are a general class that includes all well-known models except some state space and multiplicative Holt-Winters models. As originally formulated, classical ARIMA modeling attempted to capture stochastic structure in the data; little was done about incorporating deterministic structure other than a possible constant and/or identifying change points in parameters or error variance.

We will highlight procedures relevant to suggested augmentation strategies that were not part of the original ARIMA approach suggested in but are now standard. This step is often ignored as it is necessary that the mean of the residuals is invariant over time and that the variance of the final model’s errors is constant over time.  Here is the classic circa 1970.

 

 

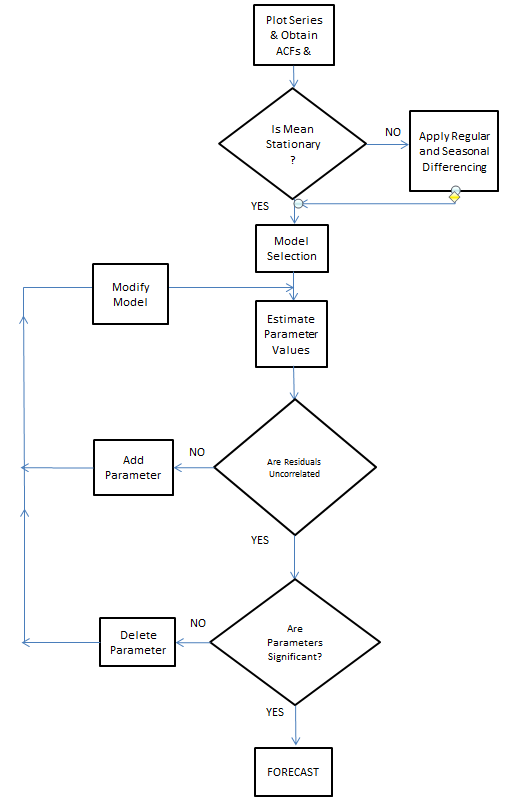
Here is the flowchart revised for additions by Tsay, Tiao, Bell, Reilly & Gregory Chow (ie chow test)

 

 

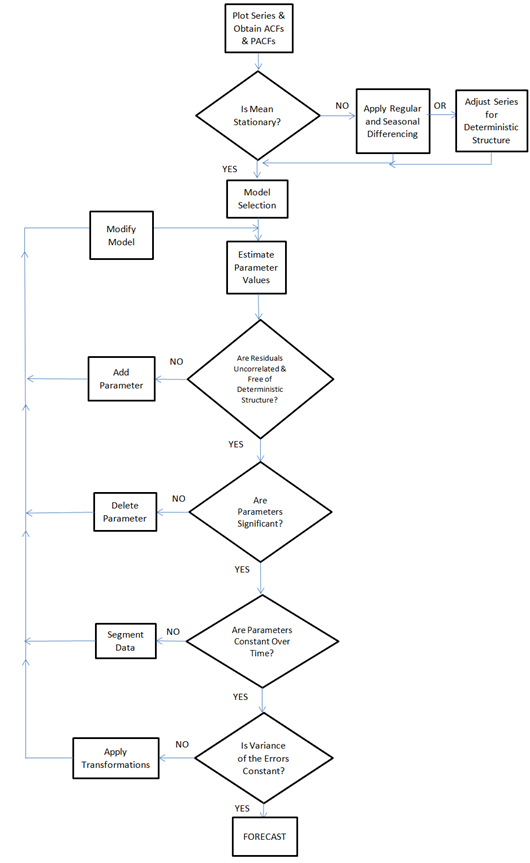
The idea of modeling is to characterize the pattern in the data and the goal is to identify an underlying model that is generating and influencing that pattern.   The model that you will build should match the history which can then be extrapolated into the future.  The actual minus the fitted values are called the residuals.  The residuals should be random around zero (i.e. Gaussian) signifying that the pattern has been captured by the model.

 

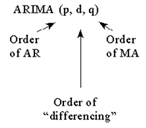
• For example, an AR model for monthly data may contain information from lag 12, lag 24, etc.

– i.e. Yt = A1Yt-12 +A2 Yt-24  + at

– This is referred to as an ARIMA(0,0,0)x(2,0,0)12 model

• General form is ARIMA(p,d,q)x(ps,ds,qs)s

 

Tools

 

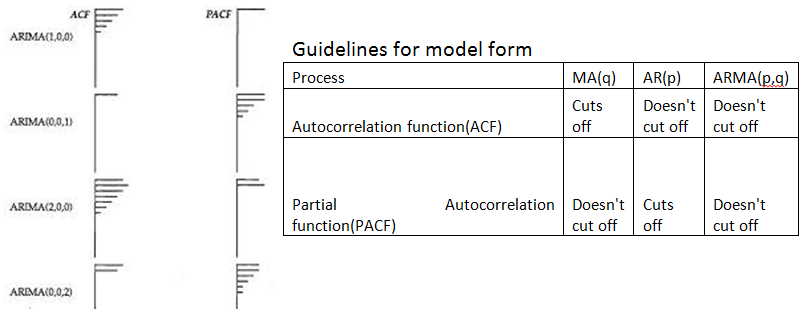
The ARIMA process uses regression/correlation statistics to identify the stochastic patterns in the data.  Regressions are run to find correlations based on different lags in the data. The correlation between successive months would be the lag 1 correlation or in ARIMA terms, the ACF of lag 1. We then examine if this month is related to one year ago at this time would then be apparent from evaluating the lag 12 correlation or in ARIMA terms, the ACF of lag 12. By studying the autocorrelations in the history, we can determine if there are any relationships and then take action by adding parameters to the model to account for that relationship. The different autocorrelations for the different lags are arranged together in what is known as a correlogram and are often presented using a plot. They are sometimes presented as a bar chart.  We present it as a line chart showing 95% confidence limits around 0.0. The autocorrelation is referred to as the autocorrelation function (ACF).

• The key statistic in time series analysis is the autocorrelation coefficient (the correlation of the time series with itself, lagged 1, 2, or more periods).

The Partial Autocorrelation Function (PACF).  The PACF of lag 12 for example is a regression using a lag of 12, but also uses all of the lags from 1 to 11 as well, hence the name partial. It is complex to compute and we won’t bother with that here.

Now that we have explained the ACF and the PACF, let’s discuss the components of ARIMA.  There are three pieces to the model. The “I” means Integrated, but it simply means that you took differencing on the Y variable during the modeling process. The “AR” means that you have a model parameter that explicitly uses the history of the series.  The “MA” means that you have a model parameter that explicitly uses the previous forecast errors. Not all models have all parts of the ARIMA model. All models can be re-expressed as pure AR models or pure MA models. The reason we attempt to mix and match has to do with attempting to use as few parameters as possible.

Identifying the order of differencing starts with the following initial assumptions, which are ultimately need to be verified:

1) The sequence of errors (a’s) are assumed to have a constant mean of zero and a constant variance for all sub-intervals of time.

2) The sequence of errors (a’s) are assumed to be normally distributed where the a’s are independent of each other.

3) Finally the model parameters and error variance are assumed to be fixed over all sub-intervals.

 

We study the ACF and PACF and identify an initial model. If this initial model is significant, the residuals will be free of structure and we are done. If not, we identify that structure and add it to the current model until a subsequent set of residuals is free of structure. One could consider this iterative approach as moving structure currently in the errors to the model until there is no structure in the errors to relocate.

 

The following are some simplified guidelines to apply when identifying an appropriate ARIMA model with the following assumptions:

• Guideline 1: If the series has a large number of positive autocorrelations then differencing should be introduced. The order of the differencing is suggested by the significant spikes in the PACF based upon the standard deviation of the differenced series. This needs to be tempered with the understanding that a series with a mean change or a trend change can also have these characteristics.

• Guideline 2: Include a constant if your model has no differencing; include a constant elsewhere if it is statistically significant.

• Guideline 3: Domination of the ACF over the PACF suggests an AR model while the reverse suggests an MA model. The order of the model is suggested by the number of significant values in the subordinate.

• Guideline 4: Parsimony: Keep the model as simple as you can, but not too simple as overpopulation often leads to redundant structure.

• Guideline 5: Evaluate the statistical properties of the residual (at) series and identify the additional structure (step-forward) required

• Guideline 6: Reduce the model via step-down procedures to end up with a minimally sufficient model that has effectively deconstructed the original series to signal and noise. Over-differencing leads to unnecessary MA structure while under-differencing leads to overly complicated AR structure.

 

 

If a tentative model exhibits errors that have a mean change this can be remedied in a number of ways;

 

1) Identify the need to validate that the errors have constant mean via Intervention Detection (2,3) yielding pulse, seasonal pulse/level shift/local time trends

2) Confirming that the parameters of the model are constant over time

3) Confirming that the error variance has had no deterministic change points or stochastic change points.

 

The tool to identify omitted deterministic structure is fully explained in references 2 and 3 as follows:

1) use the model to generate residuals

2) identify the intervention variable needed following the procedure defined in reference

3) Re-estimate the residuals incorporating the effect into the model and then go back to Step 1 until no additional interventions are found.

 

Example 1) 36 annual values:

The ACF and the PACF suggest an AR(1) model (1,0,0)(0,0,0).

 

 

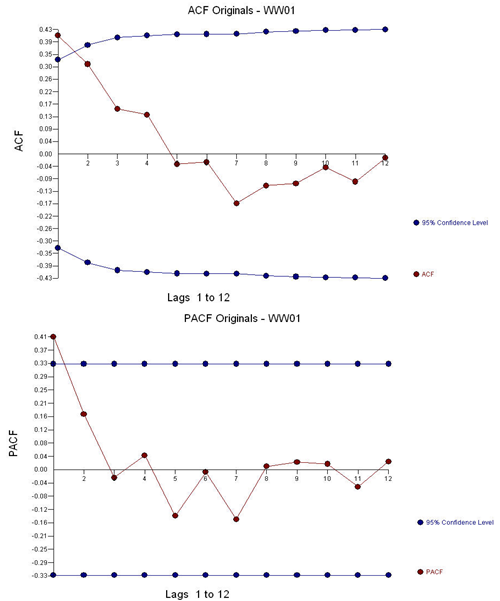
Leading to an estimated model (1,0,0)(0,0,0).

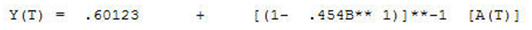
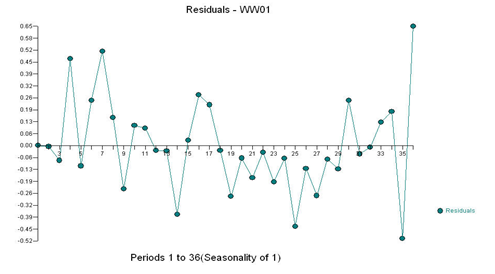
With the following residual plot, suggesting some “unusual values”:

 

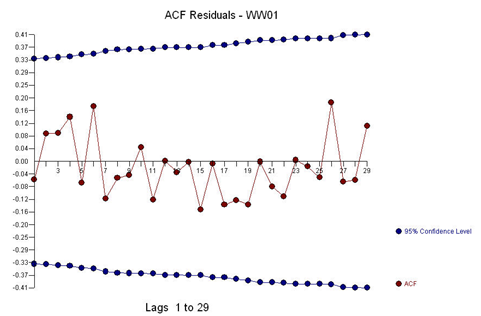
The ACF and PACF of the residuals suggests no stochastic structure as the anomalies effectively downward bias the results:

 

 

We added pulse outliers to create a more robust estimate of the ARIMA coefficients:

Example 2) 36 monthly observations:

 

 

 

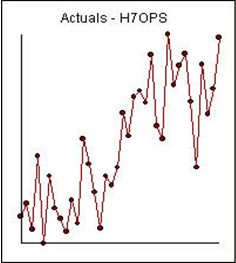
With ACF and PACF:

 

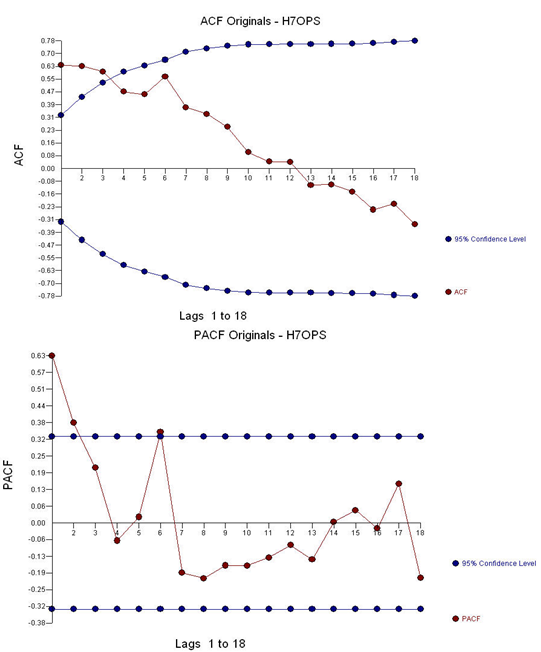
Leading to an estimated model:  AR(2) (2,0,0)(0,0,0)

 

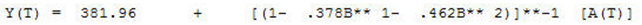
And with ACF of the residuals:

 

 

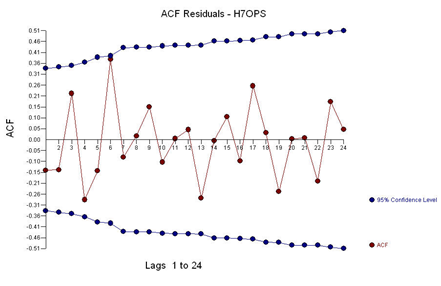
With the following residual plot:

 

 

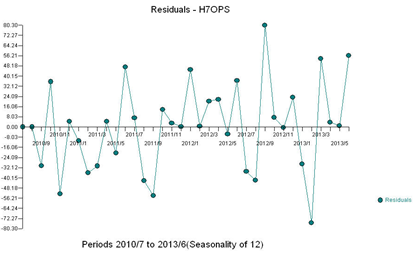
This example is a series that is better modeled with a step/level shift.

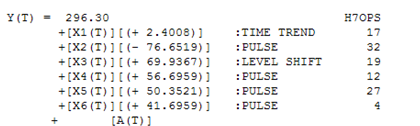
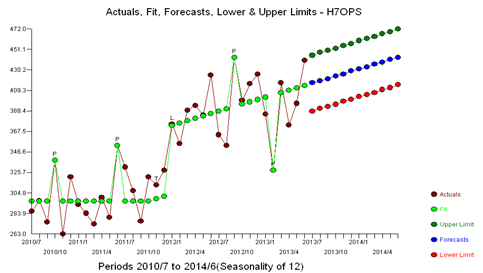
The plot of the residuals suggests a mean shift. Empowering Intervention Detection leads to an augmented model incorporating a level shift and a local time trend with and 4 pulses and a level shift. This model is as follows:

 

Example 3) 40 annual values:

 

 

The ACF and PACF of the original series are:

 

 

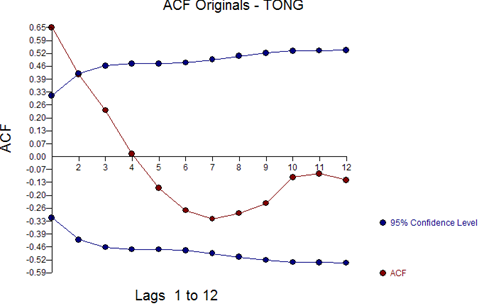
Suggesting a model (1,0,0,(0,0,0)

 

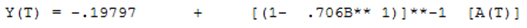
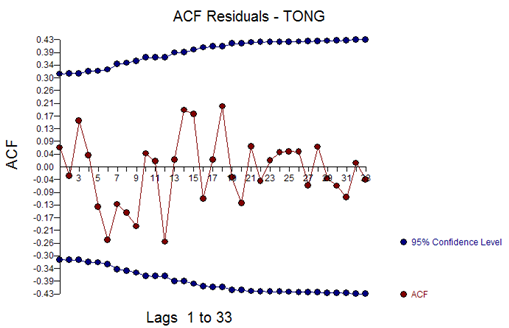
With a residual ACF of:

 

 

And residual plot:

 

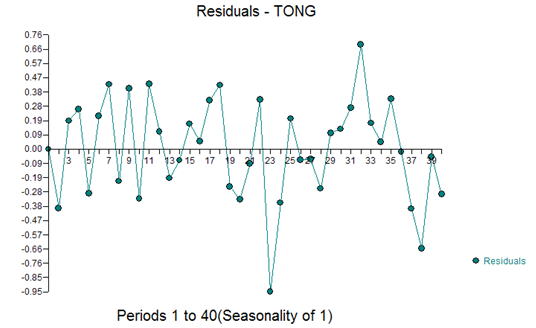
This suggests a change in the distribution of residuals in the second half of the time series.  When the parameters were tested for constancy over time using the Chow Test (5), a significant difference was detected at period 21.

 

 

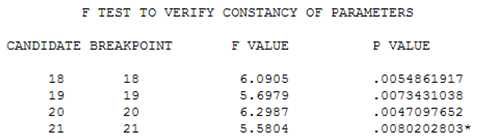
The model for period 1-20 is:

 

The model for period 21-40 is:

 

A final model using the last 20 values was:

 

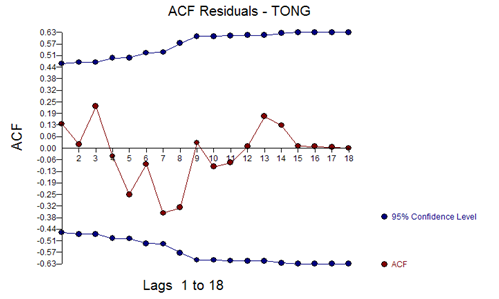
With residual ACF of:

 

 

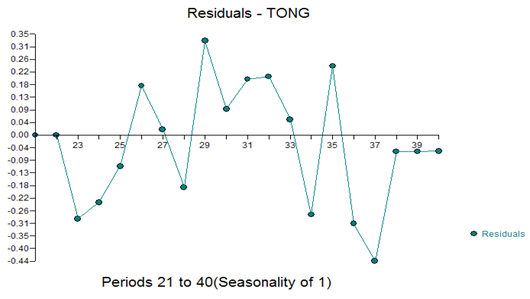
And residual plot of:

 

References

1)Box, G.E.P., and Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control, 2nd ed. San Francisco: Holden Day.

2)Chang, I., and Tiao, G.C. (1983). "Estimation of Time Series Parameters in the Presence of Outliers," Technical Report #8, Statistics Research Center, Graduate School of Business, University of Chicago, Chicago.

3)Tsay, R.S. (1986). "Time Series Model Specification in the Presence of Outliers," Journal of the American Statistical Society, Vol. 81, pp. 132-141.

4)Wei, W. (1989). Time Series Analysis Univariate and Multivariate Methods. Redwood City: Addison Wesley.

5)Chow, Gregory C. (1960). "Tests of Equality Between Sets of Coefficients in Two Linear Regressions". Econometrica 28 (3): 591–605