AN EXAMPLE OF A TWO-INPUT TRANSFER FUNCTION
USING A COMMON FILTER.
| We select three series to analyze. The dependent series is Y and the two inputs series are X1 and X2. | 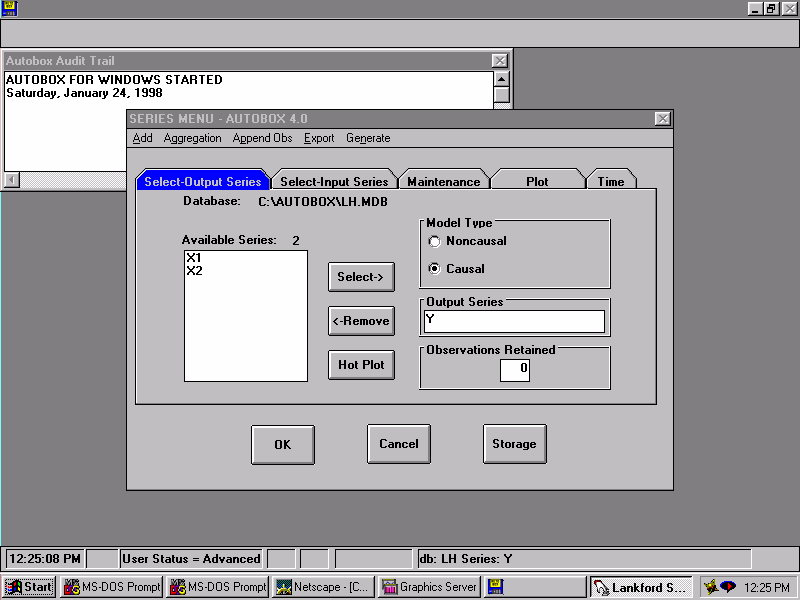 |
| We specify that we wish to review/change the Identification criteria. | 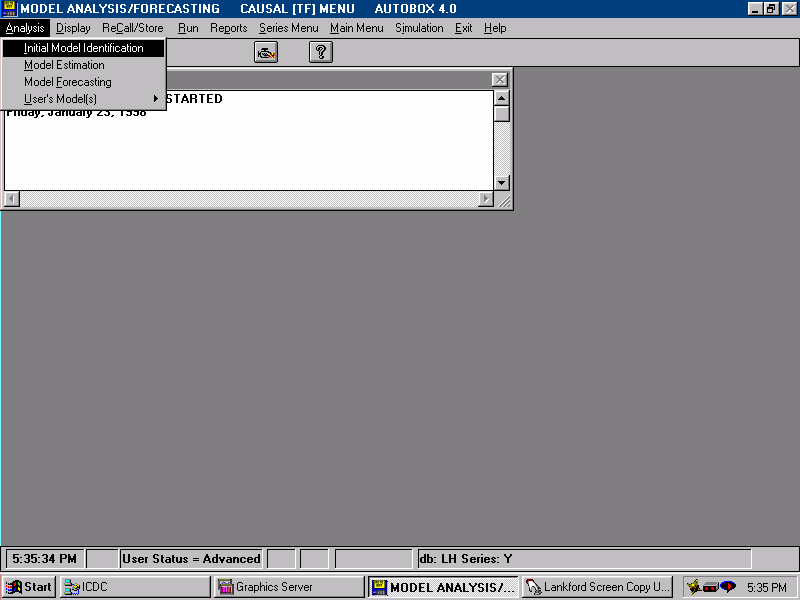 |
| We specify that we wish to use the COMMON FILTER approach to initial model identification. Essentially, this means that we will develop the impulse response weights for the two series at the same time rather than independently. | 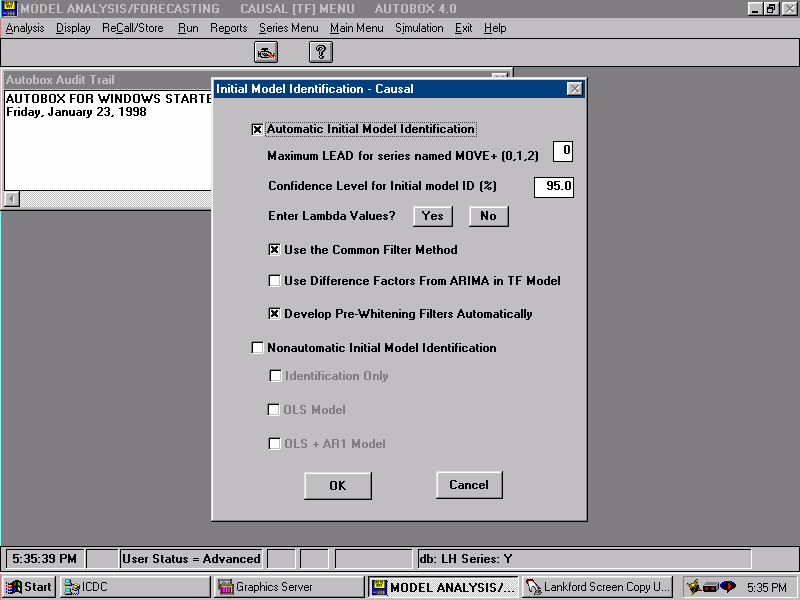 |
| We now specify the Estimation conditions. | 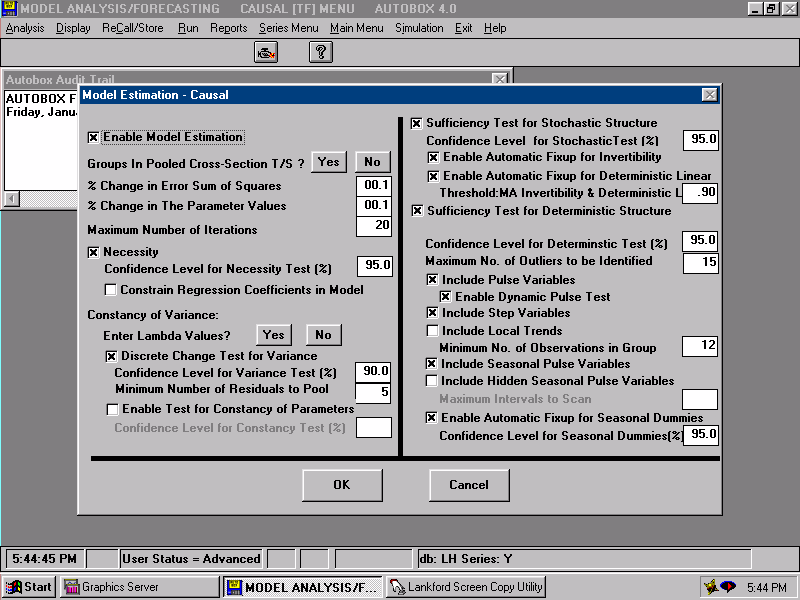 |
| A text plot of the the three series is presented. | 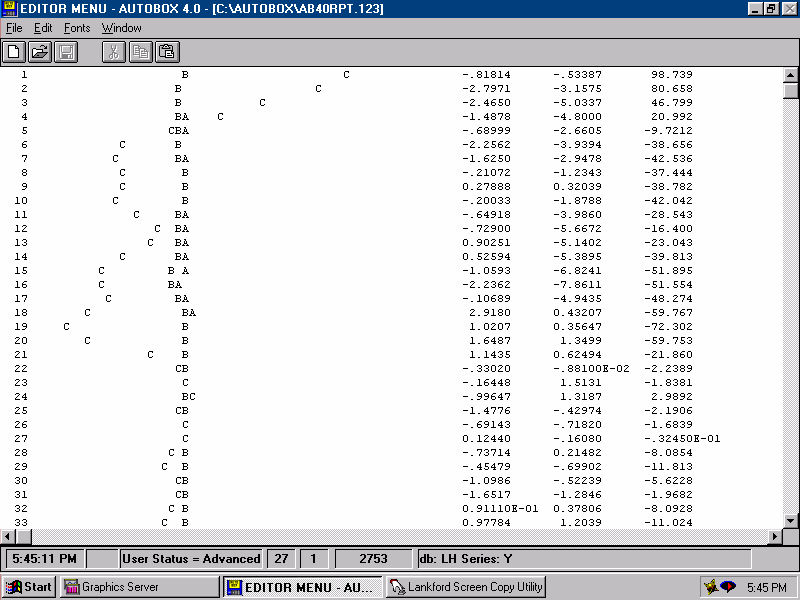 |
| In order to identify the relationship, we filter the series to more clearly "see" the form of the relationship. | 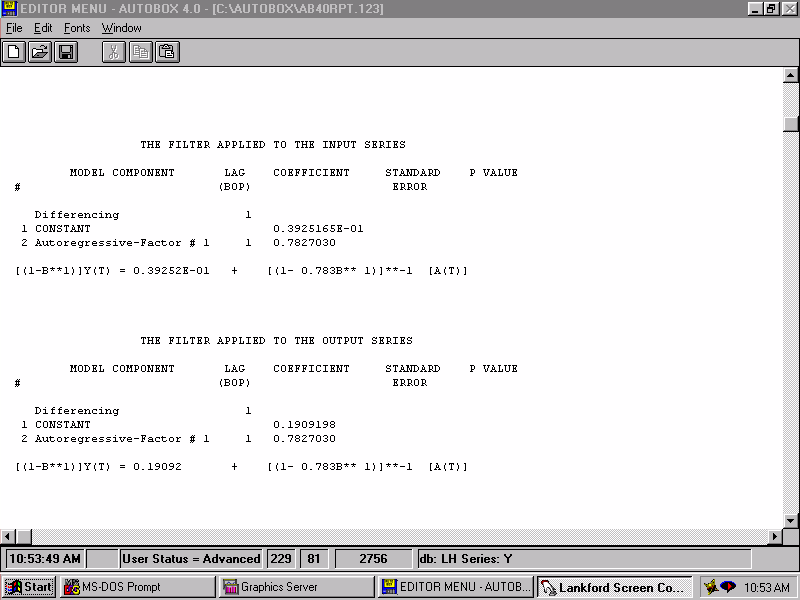 |
| The Impulse Response Weights for X1 are simply regression coefficients. | 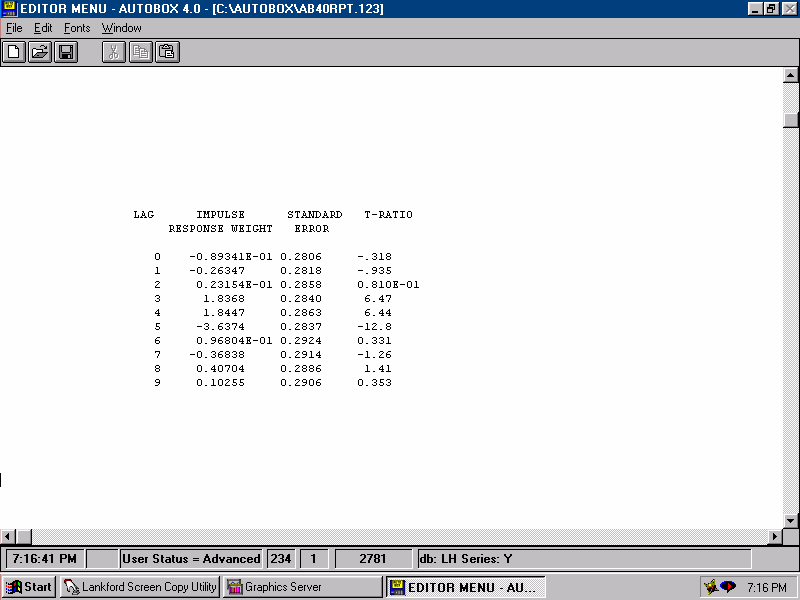 |
| The Impulse Response Weights for X2 are simply regression coefficients. | 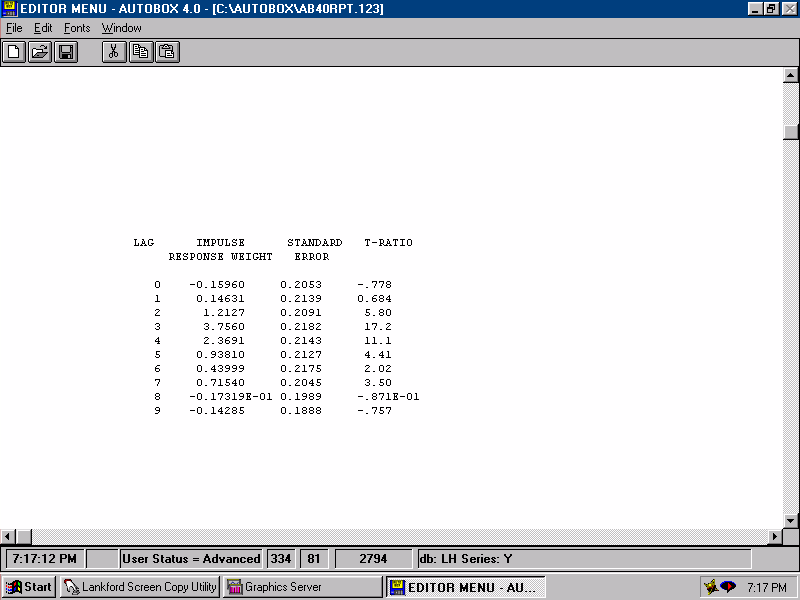 |
| After adjusting Y for the effect of the two input series, we generate a pseudo "Y" which we label as the initially identified noise process or errors. The Autocorrelation of these errors reflects omitted or unobservable variables. |
| This leads to an initial model with starting values. | 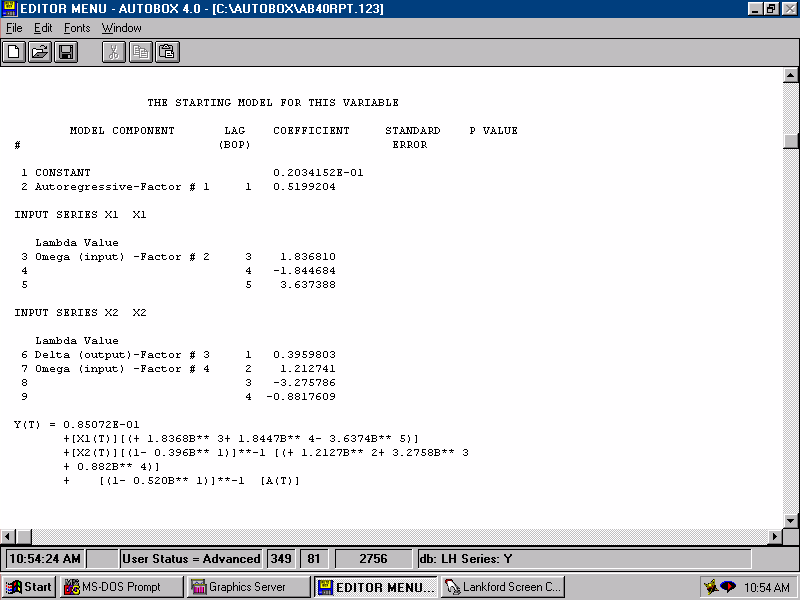 |
| Estimating we get. | 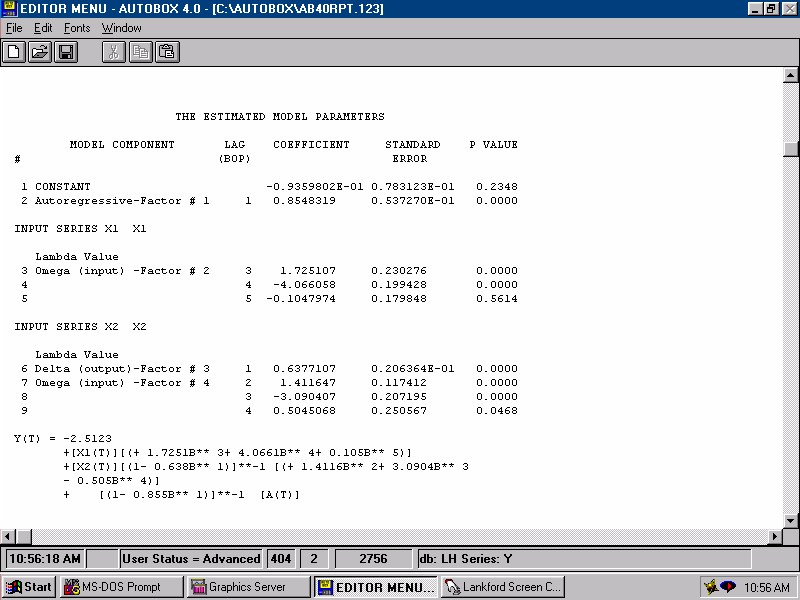 |
| The residuals from this model seem to have structure. This leads directly to an upwardly revised model. For a model to be sufficient, the errors should not be predictable by lags of the error series. If they were then we would augment the model with the evidented lag structure that was identified herein i.e. an MA(1). | 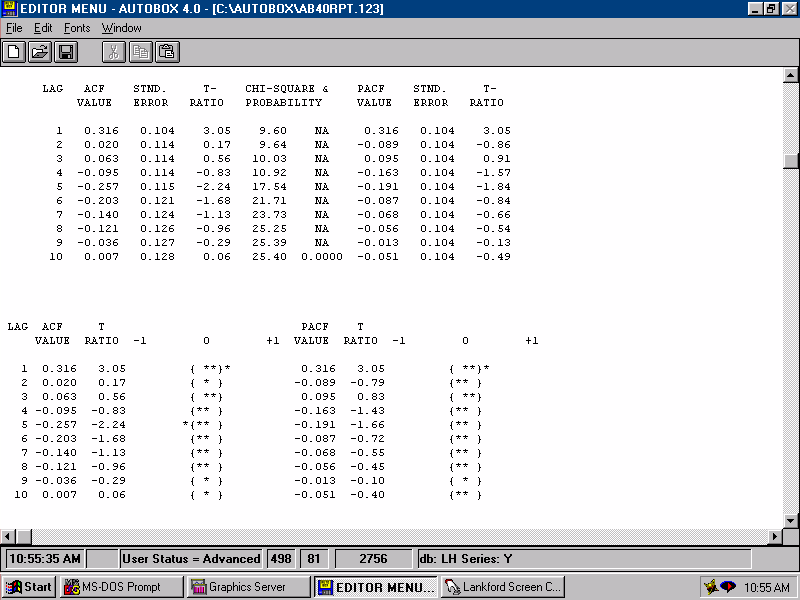 |
| Estimating this augmented model we get... | 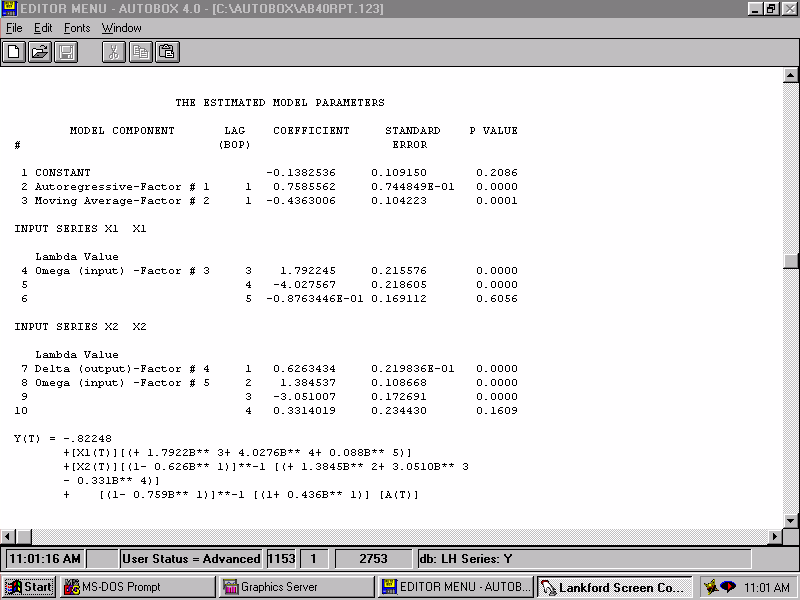 |
| After some simplification, via step-down regression, we get what appears to be a parsimonious model. Parsimony simply means that the model is as simple as possible, but not too simple. | 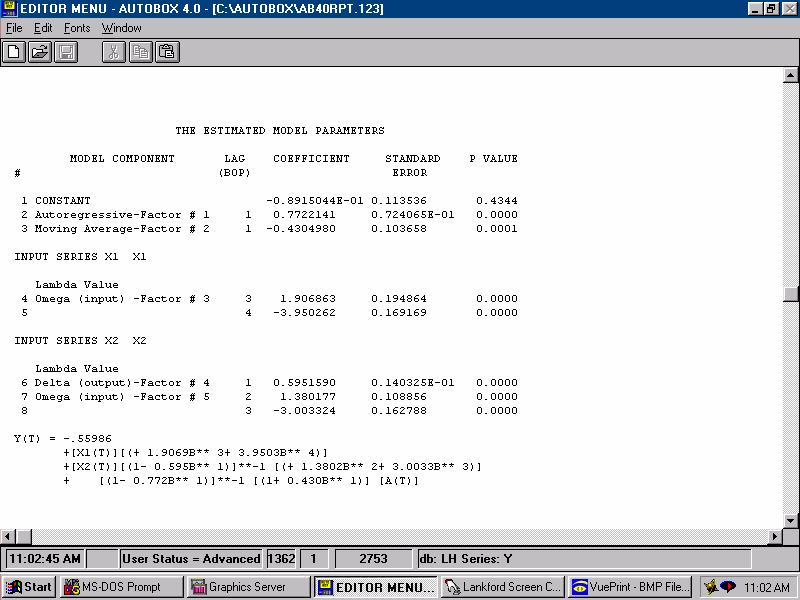 |
| For a model to be sufficient the errors should not be predictable by lags of the input series X1. If they were then we would augment the model with the evidented lag structure that was identified herein. | 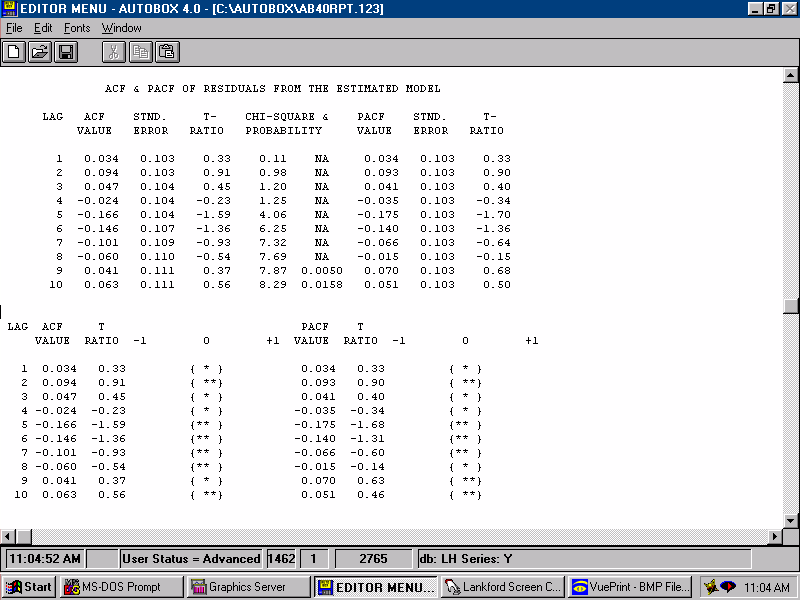 |
| For a model to be sufficient the errors should not be predictable by lags of the input series X2. If they were then we would augment the model with the evidented lag structure that was identified herein. | 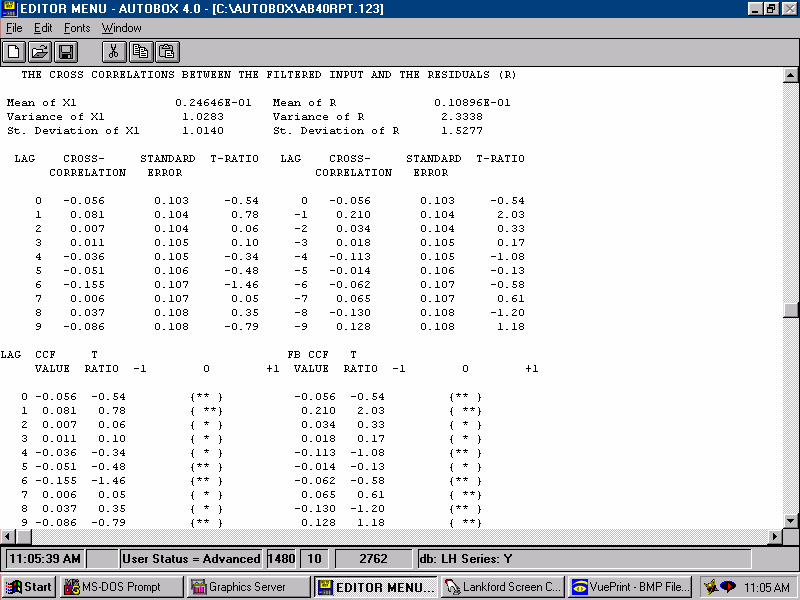 |
| For a model to be sufficient the errors should not be predictable by lags of the error series. If they were then we would augment the model with the evidented lag structure that was identified herein. |  |
| The complete analysis is detailed here. |  |
| A side bar explaining (words) why we pre-whiten to identify the relationship between an input series and an output series. |  |
| A side bar explaining (equations) why we pre-whiten to identify the relationship between an input series and an output series. |  |
| A side bar on initial identification of the TRANSFER MODEL form between Y and X1 |  |
| A side bar on initial identification of the TRANSFER MODEL form between Y and X2 |  |
| A side bar on initial identification of the TRANSFER MODEL form between Y and A |  |






