Tom Reilly
Waging a war against how to model time series vs fitting
Hey, I didn't know that ARIMA models could do that
- Font size: Larger Smaller
- Hits: 128291
- 0 Comments
- Subscribe to this entry
- Bookmark
You were taught and told through books, teachers, websites and your software that your AR model coefficient can't be outside the -1 to +1 region. This is also often stated as that "unit root" needs to be outside the unit circle, but this just isn't true. A criticism of Box-Jenkins modeling was that it wasn't applicable to growth models.
Ok, but why does that matter to me? Well, it matters to you as that means you have been operating under an assumption that limits your modeling to handle explosive data from perhaps a product launch where sales really take off. Typically, the long run forecasts from such a time series are not usually realistic, but the mid to short are useful.
Let's look at annual data that has explosive and "multiplicative" growth.
1.1 1.21 1.33 1.46 1.61 1.77 1.95 2.14 2.36 2.59 <<<<<---------- Note how the incremental differences keep getting larger(ie .11, .12, .13, .15, .16, .18, .19, .22, .23)
If we modeled this based on what we were taught or using a typical forecasting tool, it would build a model with double differencing and an AR 1. The forecasts The residuals would show that the model didn't actually capture the signal as it was constrained by the bounds of the unit circle(-1 to +1).
ARIMA(1,2,0) Coefficients: ar1 0.6868 s.e. 0.2121 sigma^2 estimated as 0.0001214: log likelihood=27.48 AIC=-50.97 AICc=-48.97 BIC=-50.57
Below are the forecasts. Note the almost flat forecast and lack of explosive growth.
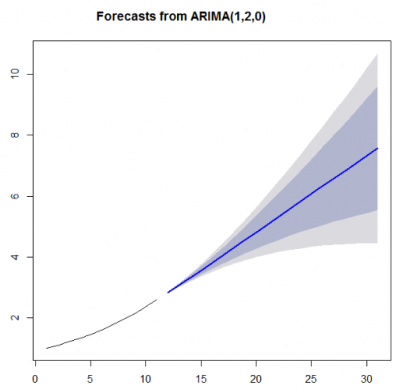
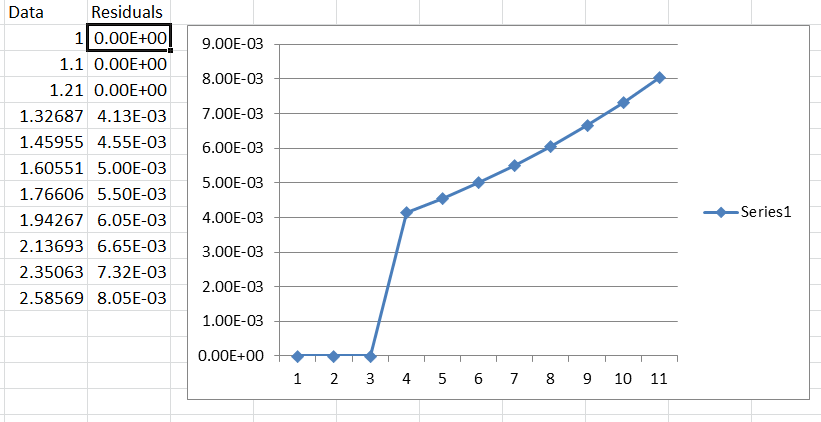
Most software and people ignore the residual plot. This is a big mistake. This is a clear way of checking to see if the model was built in a robust manner by checking if the residuals are random or also known as Normal Independently Identically Distributed (N.I.I.D.) which is the ASSUMPTION that the whole modeling process is built upon, but again ignored. The residuals are not random at all.
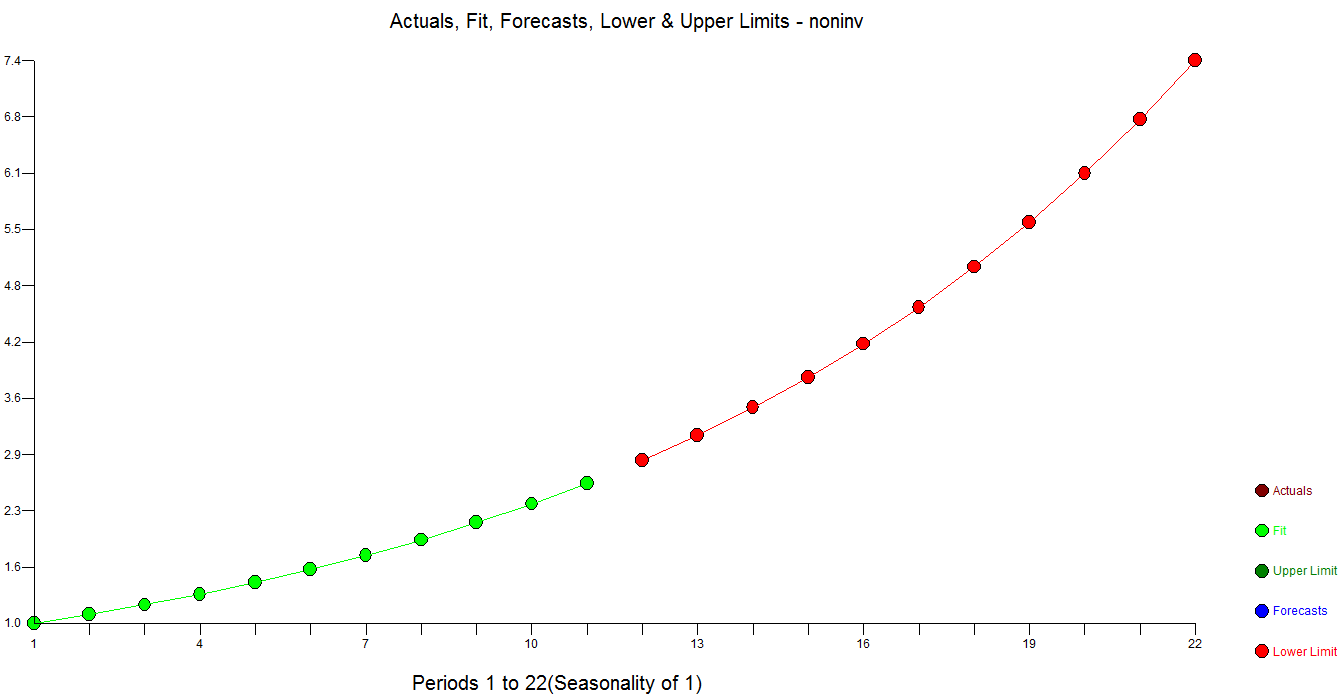
 If we ignore the unneeded unit circle constraint, the model would be again double differencing with an AR1 coefficient that is 1.1 and very much OUTSIDE the unit circle and very estimable!
If we ignore the unneeded unit circle constraint, the model would be again double differencing with an AR1 coefficient that is 1.1 and very much OUTSIDE the unit circle and very estimable!
[(1-B**1)][(1-B**1)]Y(T) = .82601E-07 + [(1- 1.1000B** 1)]**-1 [A(T)]
Comments
-
Please login first in order for you to submit comments






