Tom Reilly
Waging a war against how to model time series vs fitting
The difference between R's auto.arima and Robust Modeling. Think All Blacks vs Wallabies. Light years. Generational Gap. Neandrathal vs Human. Night and Day.
- Font size: Larger Smaller
- Hits: 119102
- 0 Comments
- Subscribe to this entry
- Bookmark
Let's evaluate auto.arima vs a Robust Solution from an example by it's author, Rob Hyndman, in his R text book.
Do this exercise in R and see for yourself!
Now, this is only one example that we are discussing here, but it reveals so much about R's auto.arima. It's a "pick best" approach of models that minimizes the AIC with no attempt to diagnose other effects like outliers, changes in level/trend/seasonality. There are many other examples we have seen that show flaws in auto.arima as we have seen them discussed on crossvalidated.com.
The data set we are examining is found in Chapter 8.5 of Rob's book called "U.S. Consumption" and it is a quarterly dataset with 164 values. Rob observes no seasonality, so he forces the model to not look for seasonality. Now this might be true, but there is something else going on here that smells funny as the name of the software is "auto", but a human is intervening. Is it really necessary to have the need for this? What consequences would happen if the user wasn't there to do this we wondered? We explore that down below.
The auto.arima generated model is an MA3 with lags 1,2,3 and a constant. All coefficients are significant and the forecast looks good so everything is great, right? Well, not really.
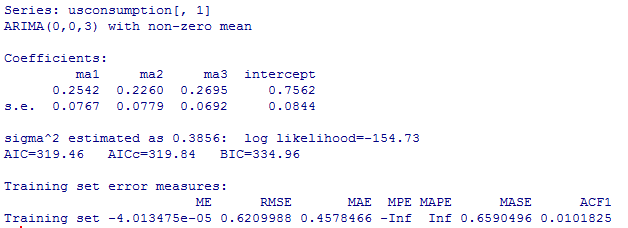
The forecasts from a Robust application(Autobox) and auto.arima end up being just about the same, but the "style" and "process" from these two tools need to be highlighted as their are stark differences in the modeling assumptions and detection of other patterns. Box-Jenkins laid out a path of Identification, Estimation, Necessity and Sufficiency with perhaps model revision and then forecasting. Auto.arima is not following this path. Auto.arima's approach is a "one and done" approach where the model is identified and that it is it.
Let's see what is really going on in terms of methodology and what assumptions are made and what is missing in auto.arima. auto.arima's process leaves a set of residuals which are obviously NOT random. The residuals show artifacts from which information can be learned about the data and perhaps a better model. Here are the auto.arima's residuals which clearly show that the first half of the data is very different from the second half. Do residuals matter? Yes. The first thing you learn when studying time series is that if the errors are not random and show pattern(s) then your model is not sufficient and needs more work.
The data is 41 years of historical Consumption and over time policy, economy and personal choice change. This data has had a change in the underlying model. Autobox detected a change in the parameters of the model and deleted the first 67 observations. Autobox uses the Chow test in time series to detect change. It's a unique feature and besides being useful in forecasting, it is also useful in detecting change in data in general. If your analysis was being done back in the periods where the change in the model really began to be noticed(the next few years after period 67) you would see a bigger difference in the forecasts between the two methods and of course right after an intervention took place.
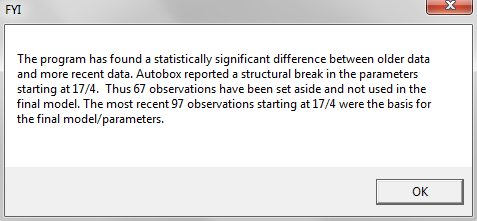
The model is different than the auto.arima in a couple more ways. Autobox finds 4 outliers and "step-ups" the model to include 4 dummy(deterministic) variables to "adjust" the data to where it should have been. If you don't do this, then you can never identify the true pattern in the data(they call this DGP-Data Generating Process). Also, there is no need for the MA1 as it is unnecessary. So, it is true that there is no quarterly effect in the data, but there is no need to "turn off" the search for seasonality.

A thank you to Michael Mostek and Giorgio Garziano for providing some R expertise in trying to run the problem and explain why Rob may have needed to turn off seasonality due to estimation problems with the ML method. Giorgio had some ideas on how to model this data, but we want to measure auto.arima's excellence and not Giorgio's.
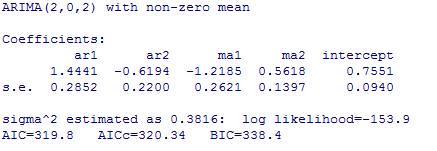
We asked a question above if there were bad consequences if a user were to allow R to look for seasonality. The answer it seems that "yes" there is a need for the user to do this override to not look for seasonality as what we found out DURING this BLOG analysis when we were just about done with this BLOG where we wondered what would happen if we were to allow auto.arima to search for seasonality?? If you do, there is a poor model and forecast. The model is fooled into believing there is seasonality as it has four seasonal parameters. It is quite a complicated model compared to what it COULD have been. It is very overparameterized. Therefore there is incorrect seasonality in the forecast. This BLOG posting on R's auto.arima time series modeling and forecasting could become a regularly occurring segment here on the Autobox BLOG. The residuals from this model are also indicative of something being missed.

What R kicks out when you run this model is an error message.
"Warning message:
In auto.arima(usconsumption[, 1]) :
Unable to fit final model using maximum likelihood. AIC value approximated
We find a remedy from crossvalidated.com when this happens which generates now a third model where you need to override auto.arima's defaults with this code
fit <- auto.arima(usconsumption[,1],approximation=FALSE,trace=FALSE)
This model relies heavily on the last value to forecast which is why the forecast is immediately high that whereas Rob's(in his book) and the model from Autobox are similar.
Please feel free to comment and hear your thoughts!!
Comments
-
Please login first in order for you to submit comments







